かんプリンの学習記録

勉強したことについてメモしています. 主に競技プログラミングの問題の解説やってます.

ABC200 E - Patisserie ABC 2

ABC 解説 競技プログラミング 形式的冪級数

問題はこちら

問題概要

全ての{1\leq i,j,k\leq N}の組{(i,j,k)}を以下のルールでソートしたときの{K}番目の値を求めよ．

上の方が優先度が高い．

  • {i+j+k}の昇順．
  • {i}の昇順．
  • {j}の昇順．

{2\leq N \leq 10^6\\ 1\leq K\leq N^3}

解説

さすがに全部列挙するのは無理．

{i+j+k}の昇順に並んでいるので，全体は以下の図のようになっている．

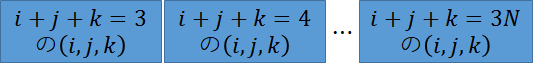
f:id:kanpurin:20210509015852p:plain:w400

{i+j+k \leq L}となる{(i,j,k)}の数を{C_L}とする．{C_L}が{K}以上となるような最小の{L}が{K}番目の{(i,j,k)}の{i+j+k}となる．
{f=(x+x^2+\cdots +x^N)}として，{\displaystyle C_L=[x^L]\frac{f^3}{1-x}}．

{L}が求まったので，{i+j+k=L}となるものの中で{K-C_{L-1}}番目のものが答えになる．

{\downarrow}

同じように{i+j+k=L}かつ{i\leq B}となるような，{(i,j,k)}の数{D_B}を求める．上の{f}を用いると，{\displaystyle D_B=[x^{L-1}]\frac{f^2}{1-x}(1-x^B)}．{D_B}が{K-C_{L-1}}以上となるような最小の{B}が{K}番目の{(i,j,k)}の{i}となる．

{B}が求まったので，{i+j+k=L}かつ{i=B}となるものの中で{K-C_{L-1}-D_{B-1}}番目のものが答えになる．

{C_x}および{D_x}は単調なので二分探索を行うと{L,B}は{O(\log N)}で求められる．

{C_x}および{D_x}は形式的冪級数で求めたが，組合せ的考えても多分解ける(形式的冪級数だと脳死で式変形するだけだから使った)．

追記
包除原理で{O(1)}でいける．{N < i}の場合とかを引いていく感じのやつ．

形式的冪級数

{\displaystyle C_L=[x^L]\frac{f^3}{1-x}}を求める．

{\displaystyle C_L=[x^L]\frac{f^3}{1-x}\\ \displaystyle =[x^{L-3}]\frac{(1-x^N)^3}{(1-x)^4}\\ \displaystyle =[x^{L-3}]\sum_{i=0}^{\infty}\binom{i+3}{3}x^i(-x^{3N}+3x^{2N}-3x^N+1)}

よって，以下の提出プログラムのように計算すれば{O(1)}で求められる．

提出プログラム

https://atcoder.jp/contests/abc200/submissions/22446038 {O(\log N)}

感想

むずい