かんプリンの学習記録

勉強したことについてメモしています. 主に競技プログラミングの問題の解説やってます.

ABC230 E - Fraction Floor Sum

ABC 典型 Python 解説 競技プログラミング

有名問題

問題はこちら

問題概要

{\displaystyle\sum_{i=1}^{N}\left\lfloor\dfrac{N}{i}\right\rfloor}を求めよ．

{1\leq N\leq 10^{12}}

解説1

答えは{xy\leq N,x>0,y>0}の領域内の格子点の数となります．({x=i}上の格子点の数は{\left\lfloor\dfrac{N}{i}\right\rfloor}になるため)
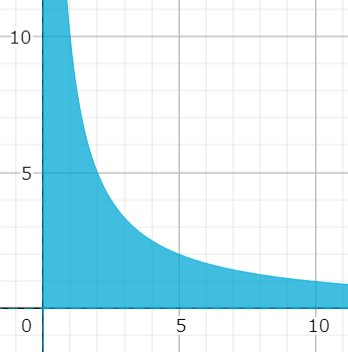
f:id:kanpurin:20211207153530p:plain:w300
N=10の例

この領域は{y=x}に関して対称であるため{y\geq x}の領域内の格子点を数えて2倍します．

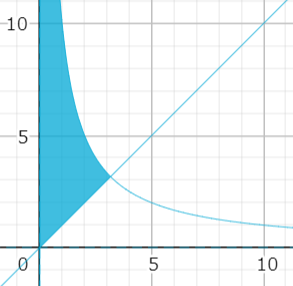
f:id:kanpurin:20211207181219p:plain
{y\leq x}
{M=\lfloor\sqrt{N}\rfloor}とします．領域内の格子点の数は
{\displaystyle\sum_{i=1}^{M}\left\lfloor\dfrac{N}{i}\right\rfloor-(i-1)=\sum_{i=1}^{M}\left\lfloor\dfrac{N}{i}\right\rfloor-\dfrac{M(M-1)}{2}}

となり，これを2倍すると
{\displaystyle 2\sum_{i=1}^{M}\left\lfloor\dfrac{N}{i}\right\rfloor-M(M-1)}

となります．{y=x}上の{M}個の格子点が2回数えられているので{M}を引いて
{\displaystyle 2\sum_{i=1}^{M}\left\lfloor\dfrac{N}{i}\right\rfloor-M^2}

が答えになります．

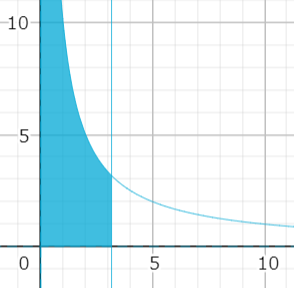
以下の領域を2倍して，2回カウントされた正方形領域の{M^2}個の格子点を引くと考えてもいいです．

f:id:kanpurin:20211207182548p:plain
{x\leq \sqrt{N}}

解説2

{\left\lfloor\dfrac{N}{i}\right\rfloor=k}となる{i}の範囲が{L\leq i\leq R}であるとします．{R=\left\lfloor\dfrac{N}{k}\right\rfloor}かつ{\left\lfloor\dfrac{N}{L}\right\rfloor=k}であるので，以下のアルゴリズムにより計算できます．

  1. {L\leftarrow 1, ans\leftarrow 0}
  2. {L\leq N}の間以下を繰り返す．
    • {k \leftarrow \left\lfloor\dfrac{N}{L}\right\rfloor}
    • {R \leftarrow \left\lfloor\dfrac{N}{k}\right\rfloor}
    • {ans\leftarrow ans+(R-L+1)×k}
    • {L\leftarrow R+1}

{L=1}から{\left\lfloor\dfrac{N}{i}\right\rfloor}が同じ値になる区間を調べていくような感じです．

  • {1\leq i\leq\sqrt{N}}のとき

　{\left\lfloor\dfrac{N}{i}\right\rfloor}としてあり得る値は{O(\sqrt{N})}個です(そもそも範囲が{O(\sqrt{N})}なので)．

  • {\sqrt{N} < i\leq N}のとき

　{1\leq \dfrac{N}{i} < \sqrt{N}}なので{\left\lfloor\dfrac{N}{i}\right\rfloor}としてあり得る値は{O(\sqrt{N})}個です．

したがって，このアルゴリズムの計算量は{O(\sqrt{N})}です．

kanpurin.hatenablog.com

提出プログラム

解説1

N = int(input())
M = int(N ** 0.5)
ans = 0
for i in range(1,M+1):
    ans += N//i
ans = 2*ans - M**2
print(ans)

解説2

N = int(input())
ans = 0
L = 1
while L <= N: 
    R = N // (N // L)
    ans += (R - L + 1) * (N // L)
    L = R + 1
print(ans)

感想