燃やす埋める纏める
この記事は競プロ Advent Calendar 2022 11日目 のために作成されました。
燃やす埋める問題として解ける制約やその他関連情報をまとめました。
他の情報も見つけ次第更新していきます。(最終更新日:2022/12/11)
燃やす埋める問題とは
燃やす埋める問題[1]の元ネタは多分こんな感じです。「燃やす/埋める」以外にも「白で塗る/黒で塗る」、「使う/使わない」などの選択肢の問題もあります。
すべてのゴミを適切に処理することで損失を最小化せよ。
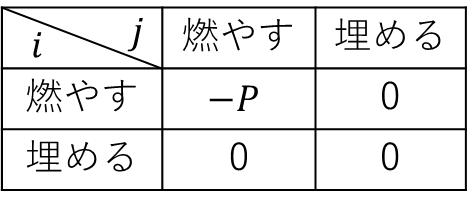
この制約はグラフカット[2]に帰着され[3]、最小カット(=最大流)が答えとなります。
具体的には、以下のようなグラフを作り、-
カット
のうち最小のものを求めればよいです。
のとき、ゴミ
を燃やすことに対応し、
のとき、ゴミ
を埋めることに対応しています。

カットエッジは赤い頂点から青い頂点への有向辺であり、最小カットは各頂点を赤or青に塗り分けるもののうちカットエッジの重みの和を最小にするようなものになります。この塗り分けが燃やすor埋めるへの割り当てと同じ意味になっています。
この「燃やす埋める」というのは日本の競プロ界隈でしか使われていません。
流行りのChatGPTも知らないみたいです()

「Project Selection Problem」と言う人もいますが、燃やす埋めると問題設定が違うと思います(解ける問題の集合は同じ)[4][5]。
単に「最小カット」としか言ってないような解説も多いです。
燃やす埋める問題として解ける制約
燃やす埋める問題として解ける制約について解説します。他にもあると思いますが分かる範囲で書いてます。
ゴミ を燃やしたとき
を燃やしたとき の損失
の損失
 のとき
のとき
ゴミそのようなグラフは頂点から頂点
に重み
の有向辺を張ることで作ることができます。

 のとき
のとき
ゴミと言い換えることができるので、次に説明する埋めたときと同様に辺を張ることができます。
例
ゴミを埋めると
の損失が発生する場合、以下のように辺を張ったグラフの最小カットの重みを求め、それに
を加えたものが問題の答えとなります。

ゴミ を埋めたとき
を埋めたとき の損失
の損失
 のとき
のとき

 のとき
のとき
ゴミゴミ を燃やしゴミ
を燃やしゴミ を埋めたとき
を埋めたとき の損失
の損失

 つのゴミの処理方法による損失
つのゴミの処理方法による損失
実は[ゴミiを燃やしゴミjを埋めたときCij(> 0)の損失]は一般化できます。ゴミ

この損失が
無条件にの損失
+ゴミを埋めると
の損失
+ゴミを埋めると
の損失
+ゴミを燃やし、ゴミ
を埋めると
の損失
これらはすでに説明した方法でグラフを作ることができます[6][7]。
 ゴミの処理方法による損失
ゴミの処理方法による損失
の場合について説明します。
これは、新たにグラフに「ゴミのうち、
つ以上が燃やされた(※)」ことを表す頂点
を追加し、(※)が真の場合
、偽の場合
になると考えると、
(※)が偽かつゴミを燃やすと
の損失
+(※)が偽かつゴミを燃やすと
の損失
+(※)が偽かつゴミを燃やすと
の損失
+(※)が真ならの損失
として表すことができます。

複数のゴミのうち つ以上が燃やされたとき
つ以上が燃やされたとき の損失
の損失
ゴミの集合先程

複数のゴミのうち つ以上が埋められたとき
つ以上が埋められたとき の損失
の損失
ゴミの集合先程と同様に考えると以下のように表現することができます。

より複雑な損失
- ゴミの集合
と
、
、
が与えられたときに、
に含まれるゴミ
のうち燃やしたゴミににおける
の和
に含まれるゴミ
のうち埋めたゴミにおける
の和
の最小値が損失となるようなグラフを作ります。
詳細は省略しますが、以下のように新たに頂点を追加し、有向辺を張ればよいです。
これが正しく損失を表現できていることは、任意の-
カット
において、このカットエッジの重みが最小となる
の割り当てを考えることで確認出来ます。
図ではに見えますが、
であっても構いません。

(
また、
は
は
は
とすることで表現できます。
したがって、上で説明した以下のつはこの損失の特殊な例と考えることができます。
複数のゴミのうち1つ以上が燃やされたときC(> 0)の損失
複数のゴミのうち1つ以上が埋められたときC(> 0)の損失
他にも、以下のようにこの構造を複数組み合わせるとより複雑な損失を表現することができます。複雑すぎる割にあまりコンテストに出てこなさそうなのでこの記事では説明しませんが、どのような損失を表すのか考えてみてください。

3つ以上の処理方法がある場合
これまでは選択肢が
これを選択肢が
ゴミの処理方法として
個の選択肢([処理
/処理
/
/処理
])があるとします。
以下の条件を満たす頂点を新たに追加します。
のとき、[処理
, 処理
,
, 処理
]のうちいずれも選ばない。
のとき、[処理
, 処理
,
, 処理
]のうちいずれかを選ぶ。
となることはないことに注意すると、以下のようなグラフを作ることができます。
は処理
を選んだ時の損失です。

が負の場合でも、無条件で
の損失を発生させ、
とすることで
とすることができます。
他にも[8]のように張る方法もあります。
2つのゴミの処理方法による損失
- 赤:
から
への有向辺
- 橙:
から
への有向辺
- 緑:
から
への有向辺
- 青:
から
への有向辺
が張られたグラフがどのような損失を表しているかを考えます。

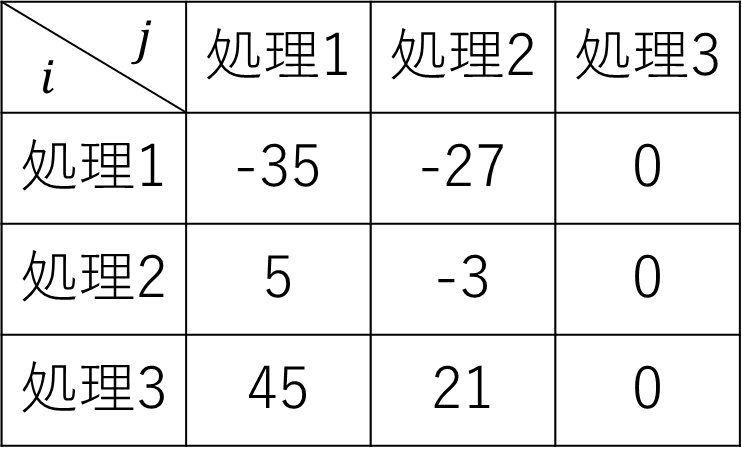
損失を表で書くと以下のようになります。辺の色と同じ色の枠の部分には一律に辺の重み分の損失が発生します。

損失をこの形に分解することができればグラフで表すこともできるということになります。例として以下のような損失をグラフで表してみます。

ゴミiを燃やしたときAiの損失やゴミiを埋めたときBiの損失を用いると、行や列から一律に値を引くことができます。
まず、ゴミに対して[処理
]を選ぶと
の損失が発生することにすると、ゴミ
の[処理
]の行から
を引くことができます。同様に[処理
/処理
]の行についても行います。
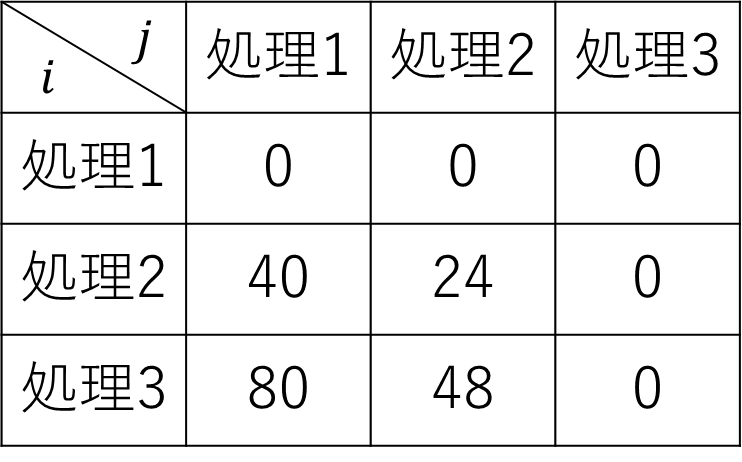
ゴミに対して[処理
]を選ぶと
の損失(
の利得)が発生することにすると、ゴミ
の[処理
]の列から
を引くことができます。同様に[処理
/処理
]の列についても行います。
先程の色枠の表を見ると、損失が次元累積和のようになっており、差分を取ることでそれぞれの辺の重みを求めることができます。

このとき、差分を取った値(右表)は非負である必要があります。
非負である条件として、損失の表(左表)内のすべてのの部分を抜き出し、値を以下のように
としたとき
であることが必要です。

∞の損失の扱い
これで機械的に解けるようになったわけですが、
実装の際、を巨大な定数として扱ってしまうと非負条件(
)が成り立たないためグラフを作ることができません。
しかし、実際には以下のようなグラフによりこの損失を表現することができます。

※これの処理方法について書きたいのですが投稿日に間に合わなさそうだったので後日書きます。
処理方法の決め方
各ゴミの処理方法は自由に決めることができます。[8]ゴミ
これを利用すると以下のような非負条件()を満たさない場合にも[2つのゴミの処理方法による損失]で説明した方法でグラフを作ることができる場合もあります。

部グラフ系の問題でこの変換を使うことがあります。
その他の損失
その他の損失を問題形式でいくつか置いておきます。重要な問題も含まれているので是非解いてみてください。ゴミ
ゴミの集合
解説
に含まれるすべてのゴミのペア
について、ゴミ
とゴミ
を燃やすと
の利得が発生するようにします(損失問題
)。
個のゴミが燃やされたとすると
の利得が発生しますが、さらに
についてゴミ
を燃やした時に
の利得が発生するものとすれば、追加で
の利得が発生し、全体で
の利得を表現するとこができます。
一般に、ゴミの集合および
が与えられているとき、
となるので、
は「
を燃やすと
の利得」、「
を燃やすと
の利得」によって表現できます。
ゴミの集合
解説
損失問題と同様に考えると3つのゴミの処理方法による損失が必要になってしまい、
の頂点や辺が追加されてしまいます。これを頂点
、辺
に抑える方法を説明します。
実は、損失の関数において
が成り立つならばグラフで表現することができます。今回の問題では
なのでこれが成り立っています。
例として、の以下のような関数
を考えます(分かりやすいように折れ線で表しています)。

結論から言うと、この関数は、
と分解できます[9]。一般に、この条件を満たす関数は正整数
を用いて
や
と表されるものの和として表すことができ、これはまさに[より複雑な損失]で説明したようにグラフで表現することができます。
答えの復元
最小カットの重みで求めた後、それぞれのゴミの処理としてどれを選んだかを求めることができます。[1]で説明されているように、各頂点が
であるか
であるかは、
が残余ネットワークにおいて始点
から到達可能であるかどうかで分かります。
計算量
最大フロー最小カット定理[10]より、最小カットを求めるには最大フローを求めればよいです。頂点
辺のグラフを考えます。
Dinic法で解く場合、計算量はとなりますが、様々な条件下でより計算量が落ちることがあります[11]。
他にも最大フローを求めるアルゴリズムとして
などがあります。
ライブラリの作成
これまでの説明をもとに燃やす埋める問題を解くライブラリを作る場合、以下のような機能があればいいと思います。ゴミの処理方法の数(必須)
各ゴミの処理方法の数ゴミの処理方法による損失(必須)
各ゴミの処理方法による損失ただし、損失が与えられた時点で辺を張るのではなく最小カットを求める直前に辺を張るようにしてください。後程説明する他の種類の損失での値が変更される場合があるためです。
 つのゴミの処理方法による損失(必須)
つのゴミの処理方法による損失(必須)
[2つのゴミの処理方法による損失]で説明した非負の条件を満たすことを関数内で確認するようにしましょう。
損失が与えられた時点で辺を張ってもいいですが、後から変更される場合もあるので注意してください。
答えの復元
ここで説明したとおりに最小カットの復元を行いましょう。頂点かつ
であるならば処理
を選んだことになります。
複数のゴミのうち つ以上が処理
つ以上が処理 をされたときの損失
をされたときの損失
たまにこの制約がある問題を見ます。任意ので
ならコレとコレで実現できます。
他にも「複数のゴミのうちすべて処理をしたら
の利得」に言い換えることもできます。
の場合にも拡張できますが、変な制約になります(素直に「
つ以上が処理
をしたら
の損失」みたいにはなりません)。
 つのゴミの処理方法における損失
つのゴミの処理方法における損失
[3つ以上の処理方法がある場合]で説明したものです。数回だけこれが必要な問題を見ました。
その他の損失
損失問題2はどこかで見たような記憶がある程度。[より複雑な損失]や損失問題3の損失は見たことないです。
流行り出したら作るくらいでいいでしょう。
練習問題
長さ

解説
各マスの選択肢は[白で塗る/黒で塗る]です。既に塗られたマスを異なる色で塗ろうとする選択にはの損失が発生するようにします。
すべてのの正方形に対して、チェックパターンなら
の利得が発生するようにしたいですが、このままではうまくできません。
ここで、となるマス
の選択肢を[黒で塗る/白で塗る]に変更すると、チェックパターンの制約が「
の正方形を形成する
つのマスすべてが選択肢
/選択肢
を選ぶ」と言い換えられるのでコレやコレが使えます。
他の問題は以下の記事にまとめています。
kanpurin.hatenablog.com